排队论模型(一):基本概念、输入过程与服务时间的常用概率分布
排队论模型(二):生灭过程 、 M / M /s 等待制排队模型、多服务台模型
排队论模型(五): 有限源排队模型、服务率或到达率依赖状态的排队模型
排队论模型(六):非生灭过程排队模型、爱尔朗(Erlang)排队模型
排队论模型(八):Matlab 生成随机数、排队模型的计算机模拟
目录
排队系统中的优化模型,一般可分为系统设计的优化和系统控制的优化。前者为静 态优化,即在服务系统设置以前根据一定的质量指标,找出参数的最优值,从而使系统 最为经济。后者为动态优化,即对已有的排队系统寻求使其某一目标函数达到最优的运 营机制。由于对后一类问题的阐述需要较多的数学知识,所以本节着重介绍静态最优问 题。
在优化问题的处理方法上,一般根据变量的类型是离散的还是连续的,相应地采用 边际分析方法或经典的微分法,对较为复杂的优化问题需要用非线性规划或动态规划等 方法。
1.M / M /1模型中的最优服务率 μ
先考虑 M / M /1/ ∞ 模型,取目标函数 z 为单位时间服务成本与顾客在系统中逗留 费用之和的期望值,即



编写 LINGO 程序如下:
![]()

编写 LINGO 程序如下:
求得系统为每位顾客最佳服务时间是0.2238h,系统每小时赢利3.70元。
2 ? M / M / s 模型中的最优的服务台数 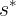 ?
?


例 13 某检验中心为各工厂服务,要求进行检验的工厂(顾客)的到来服从 Poisson 流,平均到达率为λ = 48(次/d);每天来检验由于停工等原因损失 6 元;服务(检验) 时间服从负指数分布,平均服务率为 μ = 25(次/d);每设置一个检验员的服务成本为 4 元/d,其它条件均适合 M / M / s/ ∞ 系统。问应设几个检验员可使总费用的平均值最 少?

求解的 LINGO 程序如下:
排队论模型(一):基本概念、输入过程与服务时间的常用概率分布
排队论模型(二):生灭过程 、 M / M /s 等待制排队模型、多服务台模型
排队论模型(五): 有限源排队模型、服务率或到达率依赖状态的排队模型
排队论模型(六):非生灭过程排队模型、爱尔朗(Erlang)排队模型
排队论模型(八):Matlab 生成随机数、排队模型的计算机模拟
?



